Review - (2023) Volume 11, Issue 2
An Efficient Load Balancing Algorithm for Parallel Searching and Synchronization
E. O. Bennett* and C. G. IgiriReceived: Mar 09, 2023, Manuscript No. ijcsma-22-91244; Editor assigned: Mar 11, 2023, Pre QC No. ijcsma-22-91244 (PQ); Reviewed: Mar 21, 2023, QC No. ijcsma-22-91244 (Q); Revised: Mar 25, 2023, Manuscript No. ijcsma-22-91244 (R); Published: Apr 01, 2023, DOI: 10.5281/zenodo.7827973
Abstract
In parallel tree search environments, it is likely that some nodes are heavily loaded while others are lightly loaded or even idle. It is desirable that the workload is fully distributed among all nodes to utilize the processing time and optimize the whole performance. A load balancing mechanism decides where to migrate a process and when. This paper introduces a load balancing mechanism as a novel scheme to support the reliability and to increase the overall throughput in parallel tree search environments. To alleviate the effects of processor idleness and non-essential work, a dynamic load balancing scheme called Preemptive Polling Scheme (PPS) is proposed. This scheme employs a near-neighbor quantitative load balancing method by detecting and correcting load imbalance before they occur during the search. Message Passing Interface (MPI) parallel communication model was used for inter processor communication. The search algorithm was employed to solve a Discrete Optimization Problem (DOP) (Knapsack problem) on the multi-processor system. The results show that PPS brings about scalability and efficiency in the system, as there is time reduction in the execution of the parallel tree search algorithm over its sequential counterpart is solving the DOP.
https://marmaris.tours
https://getmarmaristour.com
https://dailytourmarmaris.com
https://marmaristourguide.com
https://marmaris.live
https://marmaris.world
https://marmaris.yachts
Keywords
Parallel tree search; Dynamic load balancing; Distributed systems; Algorithms
Introduction
Very often applications need more computing power than a sequential computer can provide. One way of overcoming this limitation is to improve the operating speed of processors and other components so that they can offer the power required by computationally intensive applications. Even though this is currently possible to certain extent, future improvements are constrained by the speed of light, thermodynamic laws, and the high financial cost of processor fabrication. A viable and cost-effective alternative solution is to connect multiple processors together and coordinate their computational efforts. The resulting systems are popularly known as parallel computers, and they allow the sharing of computational task among multiple processors.
As points out; there are three ways to improve performance [1]:
• Work harder,
• Work smarter, and
• Get help
In terms of computing technologies, the analogy to this mantra is that working harder is like using faster hardware (high performance processors or peripheral devices). Working smarter concerns doing things more efficiently and this revolves around the algorithms and techniques used to solve computational tasks. Finally, getting help refers to using multiple computers to solve a computational task.
An important component of many scientific applications is the assignment of computational loads onto a set of processors. The problem of finding a task to processor mapping that minimizes the total execution time is known as mapping problem [2]. The amount of processing time needed to execute all processes assigned to a processor is called workload of a processor [3]. Load balancing strategies are used to tackle the inefficiencies of starvation and non-essential work (and hence that of memory overhead). Load balancing involves the distribution of jobs throughout a networked computer system, thus increasing throughput without having to obtain additional or faster computer hardware. Load balancing is to ensure that every processor in the system does approximately the same amount of work at any point in time [4]. An important problem here is to decide how to achieve a balance in the load distribution between processors so that the computation is completed in the shortest possible time. Since the subject of this paper is load balancing approaches, we will confine our attention to tree search spaces.
The departure from strict global-rank ordered search and a distributed memory implementation introduce several inefficiencies in parallel search algorithms:
1.1.Starvation
This is defined as the total time (over all processors) spent idling and occurs when processors run out of work.
1.2.Non-essential work
This is the total time spent processing non-essential nodes. It arises because processors perform local-rank ordered search (processors expand nodes).
• Memory overhead: This is caused by the generation and storage of non-essential nodes. Therefore, tackling non-essential work automatically takes care of the memory overhead problem.
• Duplicated work: This is the total extra time associated with pursuing duplicate search spaces and is due to inter-processor duplicates, i.e. duplicate nodes that arise in different processors, when the search space is a graph.
The above inefficiencies grow with the number of processors P used thus causing the efficiency E= T1/(P.TP) to deteriorate; here T1 denotes the sequential execution time and represents the essential work for the problem in terms of the amount of time spent processing essential nodes, and Tp denotes the execution time on Processors. We use work density to refer to the ratio T1/P.
2. Literature Review
2.1. Application of tree search algorithms
In areas like discrete optimization, artificial intelligence, and constraint programming, tree search algorithms are among the key techniques used to solve real-world problems. This section contains several examples of successful application of tree search algorithms. For instance, developed a parallel game tree search algorithm called ZUGZWANG that was the first parallel game tree search software successfully used to play chess on a massively parallel computer and was vice world champion at the computer chess championships in 1992 [5]. Applegate, Bixby, Chvatal, and Cook used a parallel implementation of branch and cut, a type of tree search algorithm [6], to solve a Traveling Salesman Problem (TSP) instance with 85,900 cities in 2006. The number of variables in the standard formulation of TSP is approximately the square of the number of cities. Thus, this instance has roughly 7 billion variables.
With the rapid advancement of computational technologies and new algorithms, one of the main challenges faced by researchers is the effort required to write efficient software. To effectively handle discrete optimization problems, there is need to incorporate problem-dependent methods (most notably for dynamic generation of variables and valid inequalities) that typically require the time-consuming development of custom implementations. It is not uncommon today to find parallel computers with hundreds or even thousands of processors. Scalability is still not easy to obtain in many applications, however, as computing environment have become increasingly distributed, developing scalable parallel algorithms has become more and more difficult.
In the following sections, we introduce some definitions and background related to tree search, parallel computing, and parallel tree search. Also, we review previous works in parallel tree search.
2.2. Definitions
This section presents the necessary background on tree search. Here, we introduce the definitions and notations relevant for describing general tree search problems and algorithms [7-9].
• A graph or undirected graph G = (N, E) consists of a set of N of vertices or nodes and a set E of edges whose elements are pairs of distinct nodes.
• A walk is an alternating sequence of nodes and edges, with each edge being incident to the nodes immediately preceding and succeeding it in the sequence.
• A path is a walk without any repetition of nodes.
• Two nodes i and j are connected if there is at least one walk from node i to
• node j.
• A connected graph is a graph in which every pair of nodes is connected.
• A tree is a connected graph that contains no cycle.
• A subtree is a connected subgraph of a tree.
• A problem is a set of decisions to be made subject to specified constraints and objectives.
• A state describes the status of the decisions to be made in a problem. e.g., which ones have been fixed or had their options narrowed and which ones are still open.
• A successor function is used to change states, i.e., fix decisions or narrow the set of possibilities. Given a particular state x, a successor function returns a set of
A node’s description generally has the following components [10]:
• State: The state in the state space to which the node corresponds;
• Parent: The node in the search tree that generated this node;
• Action: The action that was applied to the parent to generate the node;
• Path cost: The cost of the path from the root to the node; and
• Depth: The number of steps along the path from the root.
• A variety of algorithms have been proposed and developed for tree search. Tree search algorithms are among the most important search techniques to handle difficult real-world problems. Due to their special structure, tree search algorithms can be naturally parallelized, which makes them a very attractive area of research in parallel computing.
• The main elements of tree search algorithms include the following:
• Processing method: A method for computing path cost and testing whether the current node contains a goal state.
• Successor function: A method for creating a new set of nodes from a given node by expanding the state defined by that node.
• Search strategy: A method for determining which node should be processed next.
• Pruning rule: A method for determining when it is possible to discard nodes whose successors cannot produce solutions better than those found already or who cannot produce a solution at all.
To implement tree search, we simply keep the current list of leaf nodes of the search tree in a set from which the search strategy selects the next node to be expanded. This is conceptually straightforward, but it can be computationally expensive if one must consider each node in turn in order to choose the “best” one. Therefore, each node is usually assigned a numeric priority and stores the nodes in a priority queue that can be updated dynamically.
There are several reasons for the impressive progress in the scale of problems that can be solved by tree search. The first is the dramatic increase in availability of computing power over the last two decades, both in terms of processor speed and memory size. The second is significant advancements in theory. New theoretical research has boosted the development of faster algorithms, and many techniques once declared impractical have been “re-discovered” as faster computers have made efficient implementation possible. The third is the use of parallel computing. Developing a parallel program is not as difficult today as it once was. Several tools, like OpenMP, Message Passing Interface (MPI), and Parallel Virtual Machine (PVM), provide users a handy way to write parallel programs. Furthermore, the use of parallel computing has become very popular. Many desktop PCs now have multiple processors, and affordable parallel computer systems like Beowulf clusters appear to be an excellent alternative to expensive supercomputers [11-14].
2.3. Load Balancing Strategies
Load balancing strategies can have three categories based on initiation of processes:
• Sender Initiated: In this type of strategy, load transfer is initiated by the sender (donour) processor.
• Receiver Initiated: In this type of strategy, load transfer is initiated by the receiver (sink) processor.
• Symmetric: This is a combination of both sender and receiver initiated.
Depending on the current system state, load balancing strategies can be divided into two categories as static and dynamic load balancing.
2.3.1. Static Load Balancing
In these types of algorithms, no dynamic load information is used, the assignments of the tasks to the processors are made a priori using task information (arrival time, average execution time, amount of resources needed, and their inter-process communication requirements), or probabilistically. However, in reality this whole information may not be known a priori (at compile time) and this will get worse if we work in heterogeneous systems where task execution times on processing nodes will vary according to capacity of hosts.
2.3.2. Dynamic Load Balancing
The main problem with the Static load balancing is that they assume too much task information which may not be known in advance even if it is available; intensive computation may be involved in obtaining the optimal schedule. Because of this drawback much of the interest in load balancing research has shifted to dynamic load balancing that considers the current load conditions (execution time) in making task transfer decisions. So here the workload is not assigned statically to the processor, instead, this workload can be redistributed amongst processors at the runtime as the circumstances changes i.e., transferring the tasks from heavily loaded processors to lightly loaded ones.
Dynamic load balancing continually monitors the load on all participating processors, and when the load imbalance reaches some predefined level, this redistribution of workload takes place. But as this monitoring steals CPU cycles, care must be taken as to when it should be invoked. This redistribution does incur extra overhead at execution time.
2.3.3. Quantitative Load Balancing
In this approach, each processor monitors its Active Len (active nodes) periodically and reports any significant changes in it to its neighbors. Also, each processor assumes that the processor space comprises its neighbor and itself only.
Load balancing strategies are used to tackle the inefficiencies of starvation and non-essential work (and hence that of memory overhead), while duplicate pruning strategies are required to minimize duplicated work.
Since the subject of this paper is load balancing, we will confine our attention to tree search spaces.
Several methods have been proposed to achieve quantitative load balance [15-17]. Here, we critically analyses two representative schemes namely, Neighborhood Averaging (NA) and Round-Robin. In the Round-Robin (RR) strategy, a processor that runs out of nodes requests work from its busy neighbors in a round-robin fashion, until it is successful in procuring work. The donor processor grants a fixed fraction of its active nodes to the acceptor processor. The drawback of this scheme is that a number of decisions such as the next processor to request from and the fraction of work that should be granted are oblivious to the load distribution in the neighboring processor.
The Neighborhood Averaging (NA) strategy tries to achieve quantitative load balance by balancing the number of active nodes (Active-Len) among neighboring processors. For this purpose, each processor reports the current Active-Len value to its neighbors when it has changed by some constant absolute amount delta. There are two main drawbacks in this scheme. First, work transfer decisions rely solely on the load distribution around the source processor, and not that around the sink processor as well. This can give rise to two types of problems. Firstly, since this is a source-initiated strategy, it can happen that multiple source neighbors may simultaneously attempt to satisfy the deficiencies of a sink processor, thus in all likelihood converting the latter to a “source” relative to its previously source neighbors. As a result, thrashing of work will occur. Further, it is also possible for work transfer decisions to be contrary to the goal of good load balance. The second major drawback in this strategy is that load information is disseminated when absolute changes in load occur rather than percentage changes-small load changes are more important at lower loads than at heavier loads. By not taking this into account, load reports may either be too frequent (high communication overhead) or too widely spaced (poor load balancing decisions).
2.4. Isoefficiency Analysis Review
Isoefficiency analysis is also used in characterizing the scalability of parallel systems [18]. The key in isoefficiency analysis is to determine an isoefficiency function that describes the required increase of the problem size to achieve a constant efficiency with increasing computer resources. A slowly increasing isoefficiency function implies that small increments in the problem size are sufficient to use an increasing number of processors efficiently; thus, the system is highly scalable. The isoefficiency function does not exist for some parallel systems if their efficiency cannot be kept constant as the number of processors increases, no matter how large the problem size increases. Using isoefficiency analysis, one can test the performance of a parallel program on a few processors, and then predict its performance on a larger number of processors. It also helps to study system behavior when some hardware parameters, such as the speeds of processor and communication, change. Isoefficiency analysis is more realistic in characterizing scalability than other measures like efficiency, although it is not always easy to perform the analysis [19].
3. System Design
The architectural design of the Preemptive Polling Scheme is presented. The “finished available work” section in a generic load balancing architecture is replaced in Figure 1 with the “PPS”.
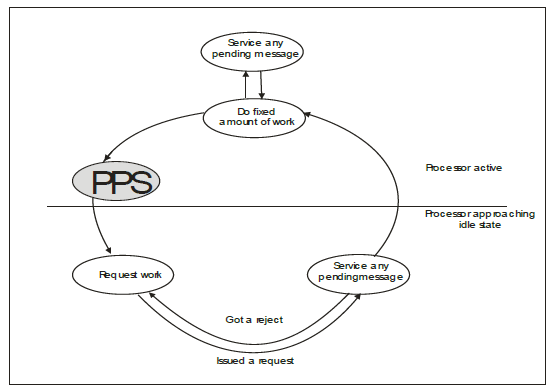
Figure 1:Preemptive Quantitative Load Balancing Architecture.
The Preemptive Polling Scheme (PPS) adopts a quantitative load balancing method to reduce idleness (idle time) and load balancing overhead. It is organized as a four-phase process:
• processor load evaluation,
• load balancing profitability
• task migration, and
• task selection/transfer
The first and fourth phases of the model are application dependent and purely distributed. Both phases can be executed independently on each individual processor. Hence, the Processor Load Evaluation Phase is reduced to a simple count of the number of tasks pending execution. Similarly, the task selection strategy is simplified since no distinction is made between tasks.
For the case where tasks are created dynamically, if the arrival rate is predictable then this information can be incorporated into the load evaluation, if not predictable, then the potential arrival of new tasks can effectively be ignored. As the program execution evolves, the inaccuracy of the task requirement estimates leads to unbalanced load distributions. The imbalance must be detected and measured (phase ii) and an appropriate migration strategy devised to correct the imbalance (phase iii). These two phases may be performed in either distributed or centralized fashion.
In our scheme, each processor monitors its (active nodes) “active-lens” periodically and reports any significant changes in it to its neighbors. In our implementation, a 10% change is reported to the neighbors. Also, each processor assumes that the processor space comprises its neighbors and itself only
Let wi = Amount of work in terms of active nodes available at processor i
Wavg,,j = Average amount of work per processor available with i and its neighbors
Let δji = wj – Wavg,j = surplus amount of work at processor j with respect to processor Wavg,j
To achieve quantitative load balance between i and its neighbors, each processor should have Wavg,j amount of work. This means that each neighbor j of i should contribute δji units of work to i which is the common pool. A negative value for δji indicates a implies a deficiency, in that case j will collect – δji units of work from i instead of contributing. Similarly, if we look at the work transfer problem from the perspective of a neighboring processor j of i, then to achieve perfect load balance between j and its neighbors, processor i should collect – δij units of work from j.
In this scheme, when a processor i preempts running out of work, it requests work from its neighbor that has i1 and has the maximum amount of work. A request for work from i to i1 carries the information δi1,j, and the amount of work generated is min (δi1,i – δi,i1), with the restriction that at least 10% and no more than 50% of the work at i1 is granted. The minimum of the two is taken because we do not want to transfer any extra work that may cause a work transfer in the opposite direction at a later time. If the work request is turned down by processor i1, say, because i1 has already granted work to another sink processor in the meantime, then processor i requests work from the processor with the next most amount of work, and so forth, until it either receives work or has requested from all its neighbor. In the latter case, it waits a certain amount of time, and then resumes requesting work as before. We will refer to work requests meant to effect quantitative load balance as quantitative load requests.
Figure 2 shows how a sink processor j3 will request work using the above quantitative load balancing scheme. From the discussion of the NA scheme, we concluded that processor j3 should actually receive work from processor j4 rather than from j2 as in the NA scheme, and thus work flows from the heavily loaded neighborhood of j4 to the lightly loaded neighborhood of j2 via processor j3.
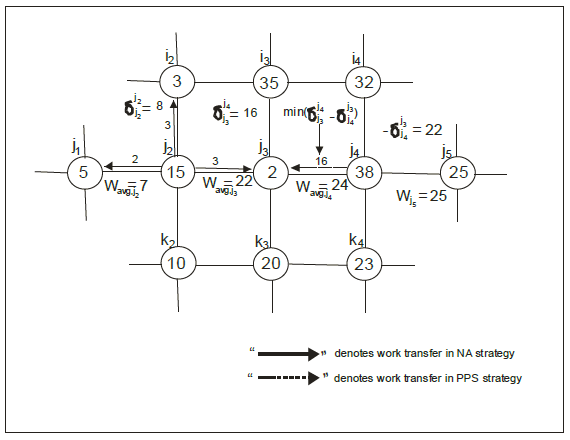
Figure 2: Work Transfer and Request Process
The NA scheme makes work transfer decisions for processor j2 considering a processor space comprising its neighbors and itself. i.e. a processor space of radius one. On the other hand, our quantitative load balancing scheme makes work transfer decisions for processor j3 considering a processor space comprising its neighbors, its neighbor’s neighbor (since the average neighborhood load of the neighbors is taken into account), and itself, i.e. a processor-space of radius two.
To reduce idling caused by latency between work request and work procurement, processors issue quantitative work requests when starvation is anticipated as follows: We note that at any time the least-cost node in a processor is expanded. Therefore, any decrease in active-len below a low threshold implies that the best nodes available are not good enough to generate active nodes and hence this decrease is likely to continue. In this scheme, processors start requesting nodes when active-len is below a certain low threshold. The acceptor threshold, and it is decreasing. It is found that this prediction rule works very well in practice. Using such a look-ahead approach, we are able to overlap communication with computation. Moreover, the delay due to transfer of a long message can be mitigated by pipelining the message transfer, i.e., by sending the work in batches.
Basically, the first message unit should be short, so that the processor does not idle long before it receives any work. Subsequent messages (for the same work transfer) can be longer but should not be so long that the preceding message unit gets consumed and the processor idles for an appreciable period of time. For the problem sizes we experimented with, it sufficed to use a short message (one or two nodes) followed by longer messages (each not exceeding 20 nodes).
Note that we perform quantitative load balance only when a processor is about to starve, not all times as in the NA scheme. Thus, our quantitative load balancing scheme overhead is low. Figure 3 shows the process flow for the PPS.
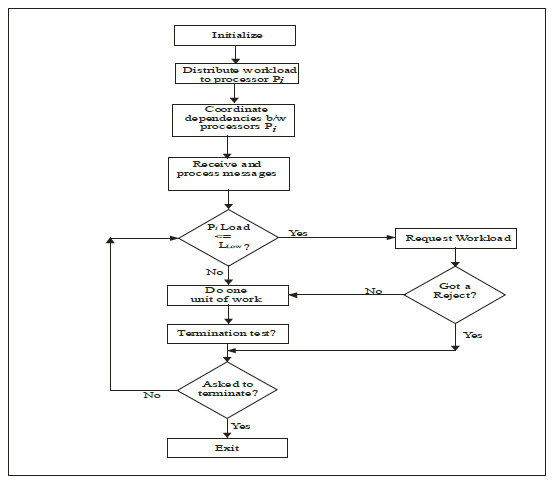
Figure 3: Algorithm Flow for Preemptive Polling Scheme
4. Algorithm 1: Parallel Search with PPS
• Initialize: //set all initial conditions for the search
• Partition search space: // Master assigns partitions to available processors
• Coordinate dependencies between processors
• Construct priority queue for partitions local to each process
• Parallel tree search // best-first local search
• Each processor i , 0
• Report work status: periodically monitor active-len and the threshold cost, and report significant changes (10% and greater) in them to all neighbors
• Receive work report: report and record work status
• Update j-max and j-best: j-max = neighbor with max active-len value; and j-best = neighbor with least threshold cost
• Work request:
• If (no prev work request from i remains to be serviced) then
• Begin
• If (active-len=0) or < acceptor threshold and is decreasing)
• Send a quantitative work request to j-max, along with information δi j-max
• Else if (lead-node is costlier than threshold cost of j-best)
• Send a qualitative work request to j-best, along with the cost of lead-node
• Endif
• Donate work: if (a quantitative work request is received from neighbor j) then grant min (δij-δji) (but at least 10% and not more than 50% of active-len) active nodes in a pipelined fashion
• Donate work: if (a qualitative work request is received from neighbor j) then grant a few active nodes that are cheaper than j’s lead node
• Receive work: if (work is received) then insert t nodes received in OPEN
• Process the node i
• Apply pruning rules:
• if (Node I cannot be pruned) then
• Create successor of node I on successor function and add to i
• Else (Prune node i)
• Do termination test?
• Exit
4.1. Time Complexity Analysis
Let W = number of states expanded by serial algorithm
Wp = number of states expanded by parallel algorithm
Search Overhead = Wp/W describes the overhead due to the order in which states are expanded.
For uninformed search, it is often possible to observe speedup anomalies where:
Wp/W<1 due to the parallel algorithm searching in multiple regions simultaneously. For informed search the situation is reversed, and the search overhead is added on top of the usual parallel overheads. Since we can compute neither W nor Tp. We express T0 in terms of W and use P*Tp = W + T0
4.2. Assumptions
Communication subsumes idling (i.e. quantify number of requests). Work can be divided into pieces as long as it is larger than a threshold ÃÂ?. The work-splitting strategy is reasonable. Whenever work ω is split into two parts ψω and (1 – ψ)ω, there exists an arbitrary small constant 0 < α ≤ 0.5 such that ψω > αω and (1 – ψ)ω > αω. (In effect, the two pieces are not too imbalanced).
The consequence of the above assumptions: if a processor initially had work ω, then after one split neither processor can have more than (1 – α)ω work.
Let V(p) be the total number of work requests before each process receives at least one work request. If the largest piece of work at any time is W, then after V(p) requests, a processor cannot have more than (1- α)W work (i.e., each processor has been the subject of a split at least once).
After 2V(p) requests, no more than (1- α)2 W work, and so on.
After (log1/(1- α) (W/ ÃÂ?))V(p) requests, no processor has more work than the threshold ÃÂ?. Conclusion: total number of work requests is O(V(p)log W)
V(P) for Preemptive Polling Scheme (PPS):
Let F(i,p) be a state in which i of the P processes have received a request and P-i have not.
Let f(i,p) be the average number of trials required to change from state F(i , p) to F(P, P)
V(P) = f(0,p)
F(p,p) = 0
F(i,p) = 1/p (1 + f(i , p)) + p-i/p (1+f(i +1, p)), (p-i /p) f(i,p) = 1 + p-i ,p), f(i,p) = p /p-i + f(i+1,p)
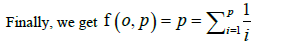
the harmonic series is roughly 1.69ln p, so
V(P) = O (plogp)
4.3. Isoefficiency Analysis
4.3.1. For Neighborhood Averaging (NA)
T0 = O(V(p)log W
T0 = O(V(p)logW)
Since V(P) = O(p2 )
It follows that:
W = O(P2 log W)
= O(P2 log(P2 log W)
= O(P2 logP + P2 log log W)
= O(P2 log P)
4.3.2. For Global Round-Robin (GRR)
T0 = O(V(P)log W)
Since V(P) = O(P)
It follows that
W = O(P log P) However, this does not account for the contention at the global counter. The counter is incremented O(PlogW) times in O(W/P) time.
This gives
W/P = O(PlogW)
And W = O(P2 logP) which is the Isoefficiency
4.3.3. For Preemptive Polling Scheme (PPS)
T0 = O(V(P)log W)
Since V(p) = O (P log P)
It follows that:
W = O(P log P log W) = O(P log2 P)
From the above analysis, AN has poor performance due to its many requests while GRR suffers from contention. PPS provides is a suitable compromise.
5. Implementation
5.1.Implementation Paradigm
The master-worker paradigm is used here for implementing tree search because a search tree can be easily partitioned into a number of subtrees. In fact, there are not many studies in parallel tree search that use other paradigms other than master-worker. In designing the control strategy of the algorithm, we let the master generate the initial nodes needed during the ramp-up phase, and distribute to the workers who will also have their own local node pools. Although, this paradigm comes with its problems, it is suitable for our implementation because of the size of system used.
5.2.Hardware and Test Environment
The physical architecture used is the tests is a network-based system, comprising 16 Sun Ultra 16 Workstations, physically connected by switched 100 Mbit Ethernet. The experiment used a set of systems comprising 2.8GHz Pentium processors and 2GB of RAM. We limited each processor to one parallel process
To reduce communication demands and alleviate potential network contention, we only use point-to-point local communication functions to implement the parallel system. The parallel search algorithm and test problems were implemented in C++ using MPI protocol for inter-processor communication.
5.3.Test Suite
Eight knapsack instances were generated based on the algorithm proposed by [19]. We tested the eight instances of the knapsack in Table 1 by using 4, 8, and 16 processors system. The default algorithm was used to solve the eight instances. The number of nodes generated by the master was 3200 and the number of nodes designated as a unit of work for 8 processors is 400. Few of the instances were difficult to solve sequentially, but they were all solved to optimality quite easily using just 4 processors. When we increased the number of processors used to 16, the system was able to solve the instances to further reduced time as shown in Table 2. Table 1 shows basic statistics for the eight instances when solving them sequentially. Column Item is the number of items available to be placed in the knapsack. Column Best Sol is the path cost of the best solution found. Column Node is the number of nodes processed and column Node Left is the number of nodes left when solving serially using the application developed from our algorithm with a time limit of 3000 seconds. We chose 3000 as the time cutoff, since the program can solve most knapsack instances within the range in this amount of time. The last column Time shows the wall clock time in seconds used for each instance.
Table 1. Table of the knapsack instances with sequential algorithm
| Instance | Item | Best Sol | Nodes | Node Left | Time |
|---|---|---|---|---|---|
| Input100a | 100 | 19387 | 19489172 | 0 | 2696 |
| Input100b | 100 | 18024 | 7334000 | 346716 | 3000 |
| Input100c | 100 | 18073 | 6078869 | 0 | 1763 |
| Input100d | 100 | 9367 | 4696000 | 3290611 | 3000 |
| Input75a | 75 | 6490 | 13858959 | 0 | 2874 |
| Input75b | 75 | 8271 | 13433001 | 0 | 1233 |
| Input75c | 75 | 8558 | 18260001 | 724141 | 3000 |
| Input75d | 75 | 8210 | 9852551 | 0 | 2672 |
Table 2. Scalability of solving 8 knapsack instances.
|
P |
Node |
Ramp-up |
Idle |
Ramp-down |
Wall clock |
Eff |
|---|---|---|---|---|---|---|
|
4 |
193057493 |
0.36% |
0.03% |
0.02% |
52.46 |
1.00 |
|
8 |
192831731 |
0.82% |
0.09% |
0.08% |
26.99 |
0.97 |
|
16 |
192255612 |
1.67% |
0.33% |
0.38% |
14.08 |
0.93 |
The table shows that the algorithm could not solve instances input 100b, input 100d and instance 75c within the 3000 seconds time limit.
We tested the eight instances of the knapsack in Table 2 by using 4 processors, 8 processors and 16 processors system. The default algorithm was used to solve those instances. The number of nodes generated by the master was 3200 and the number of nodes designated as unit of work is 400.
Although a few of these instances were difficult to solve sequentially, they were all solved to optimality quite easily using just 4 processors. As shown in Table 1, instances input 100c, input 100e, and input 75c are unsolvable with the sequential application in 3000 seconds. However, it took the same program application 128.30 seconds, 67.50 seconds, and 42.43 seconds to solve them respectively when using 4 processors. When we increased the number of processors used to 16, the application was able to solve them in 34.17 seconds, 18.24 seconds, and 11.47 seconds respectively. Because the results of the 8 instances show similar pattern, we aggregate the results, which are shown in Table 2. The column headers have the following interpretations.
• Nodes: Is the number of nodes in the search tree. Observing the change in the size of the search tree as the number of processors is increased provides a rough measure of the amount of redundant work being done. Ideally, the total number of nodes explored does not grow as the number of processors is increased and may actually decrease in some cases, due to earlier discovery of feasible solutions that enable more effective pruning.
• Ramp-up: Is the average percentage of total wall clock running time each processor spent idle during rampup phase.
• Idle: Is the average percentage of total wall clock running time each processor spent idle due to work depletion, i.e., waiting for more work to be provided.
• Ramp-down: Is the average percentage of total wall clock running time each processor spent idle during the ramp-down phase.
• Wall clock: Is the total wall clock running time (in seconds) for solving the 8 knapsack instances.
• Eff: Is the parallel efficiency and is equal to the total wall clock running for solving 10 instances with p processors divided by the product of 4 and the total running time with four processors. Note that the efficiency is being measured here with respect to solution time on four processors, rather than one, because of the memory issues encountered in the single-processor runs.
The parallel efficiency is very high if computed in the standard way (see Equation 1). To properly measure the efficiency of our algorithm (application) we use the wall clock on 4 processors as the base for comparison. We therefore define efficiency here as
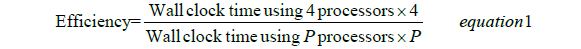
The experiment shows that our algorithm scales well, even when using more processors (i.e. to the number of processors we have used to test it).
6. Effect of Preemptive Polling Scheme
Again, to test the effectiveness of the dynamic load balancing (preemptive polling scheme) as against a situation where there is no load balancing, we performed different sets of experiments to ascertain this. Table 3 shows the results of searching with and without dynamic load balancing enabled. Column balance indicates whether dynamic load balancing scheme was enabled or not. Other columns have the same meaning as those in Table 2. As expected, using PPS load balancing helped reduce overhead and reduce solution time for all instances. The results reconfirm that dynamic load balancing (in this case, the Preemptive Polling Scheme) is important to the performance of a parallel search algorithm.
Table 3. The Effect of PPS load balancing on knapsack instances.
| P | Balance | Node | Ramp-up | Idle | Ramp-down | Wallclock |
|---|---|---|---|---|---|---|
| 4 | No | 10771651 | 0.43% | 0.00% | 49.61% | 87.60 |
| Yes | 16503223 | 0.57% | 0.07% | 0.16% | 26.02 | |
| 8 | No | 13791025 | 0.44% | 0.00% | 39.80% | 70.18 |
| Yes | 11535858 | 1.00% | 1.00% | 0.08% | 18.01 |
Conclusion
Parallel programming field lacks a common development direction. Tree search problems are examples of the formulation of Discrete Optimization Problems (DOP). We have proposed a novel dynamic load balancing scheme for parallel search called Preemptive Polling Scheme (PPS). Comparative analysis of PPS with other studied dynamic load balancing schemes suggests that PPS is a desirable balance. An appropriate method for the sharing of workload is a critical choice to make in parallel search problems. The expressive power of the PPS has been investigated in-depth both theoretically and empirically. The experiment shows that the introduction of PPS improves the overall load balancing of the system, and does not introduce significant overhead, in terms of execution time, even if it requires the exchange of a higher number of messages between nodes. Future expansions to this include extensive/expansion of the number of nodes.
References
- Pfister GF. “In search of clusters”. Prentice-Hall Inc. (1998).
- Helmy, T., et al. "A Framework for Fair and Reliable Resource Sharing in Distributed Systems." Distrib Parallel Syst: Focus Deskt. Grid Comput. (2008): 115-128.
- Kunz, Thomas. "The influence of different workload descriptions on a heuristic load balancing scheme." IEEE trans softw eng. 17.7 (1991): 725-730.
- Xu, C-Z., and Francis C. M. Lau. "Optimal parameters for load balancing using the diffusion method in k-ary n-cube networks." Inf Process Lett. 47.4 (1993): 181-187.
- Luling, R., & Burkhard, M. "Load balancing for distributed branch & bound algorithms." IEEE, (1992).
- Padberg, Manfred, & Giovanni R. "A branch-and-cut algorithm for the resolution of large-scale symmetric traveling salesman problems." SIAM rev. 33.1 (1991): 60-100.
- Sanders, Peter. "Tree shaped computations as a model for parallel applications." ALV’98 Workshop appl. based load balanc. (1998).
- Korf, Richard E. "Artificial intelligence search algorithms." (1999): 22-17.
- Cormen, Thomas H., et al. "CS702: Advanced Algorithms Analysis & Design." J Assoc Comput Mach. 34.3 (1987): 596-615.
- Russell, Stuart J. Artificial intelligence a modern approach. Pearson Educ Inc. (2010).
- Chapman, B., et al. Using OpenMP: portable shared memory parallel programming. MIT press, (2007).
- Balaji, Pavan, et al. "MPI on millions of cores." Parallel Process. Lett. 21.01 (2011): 45-60. [Google Scholar]
[CrossRef]
- Dinan, James, et al. "Supporting the global arrays PGAS model using MPI one-sided communication." IEEE, (2012).
- Geist, Al, et al. “PVM: Parallel virtual machine: a users' guide and tutorial for networked parallel computing.” MIT press, (1994).
- Mahapatra, Nihar R., and Dutt, S. "Scalable duplicate pruning strategies for parallel A* graph search." IEEE, (1993).
- Saletore, Vikram A. "A distributed and adaptive dynamic load balancing scheme for parallel processing of medium-grain tasks." IEEE. 2. (1990).
- Sinha, Amitabh B., and Laxmikant V. "A load balancing strategy for prioritized execution of tasks." IEEE, 1993.
- Grama, Ananth Y., et al. "Isoefficiency: Measuring the scalability of parallel algorithms and architectures." IEEE. 1.3 (1993): 12-21.
- Martello, Silvano, and Paolo Toth. "Algorithms for knapsack problems." N.-Holl. Math. Stud. 132 (1987): 213-257.
[Google Scholar] [CrossRef]