International Journal of Computer Science and Mobile Applications

Complexity of Negation Domains, Swarm Optimization, Fractal Numbers and Experimentation

Mirzakhmet Syzdykov^* Satbayev University, Almaty, Kazakhstan
^*Correspondence: Mirzakhmet Syzdykov, Satbayev University, Almaty, Kazakhstan, Email:

Received: Apr 03, 2023, Manuscript No. ijcsma-23-93971; Editor assigned: Apr 05, 2023, Pre QC No. ijcsma-23-93971 (PQ); Reviewed: Apr 19, 2023, QC No. ijcsma-23-93971 (Q); Revised: Apr 25, 2023, Manuscript No. ijcsma-23-93971 (R); Published: May 02, 2023, DOI: 10.5281/zenodo.7956014

Introduction

The extended regular expressions or ERE were first presented in after which we have distinguished the exact algorithm which is coherent to the labeling of the AND-operator in the source language while it’s closed under intersection of arbitrary languages within the defined set of symbols or alphabet – these ERE aren’t closed under some extensions, however, are closed under intersection operator [1-3].

We define the naming of the domain in ERE for subtraction and complement operators as well as the last operator can be re-written according to the following equation:

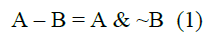
Typically, the operator “~”, or complement, can be constructed using the on-the-fly approach when the deterministic finite automata or DFA is defined during the local search and its starting and accepting states are changed accordingly.

Rabin and Scott presented a good example of using terms non-determinism and determinism for subset construction, thus, converting non-deterministic finite automata or NFA into corresponding DFA without the loss of regular language described by input regular expression [4].

We use the extension of the above method in order to defined the modified subset construction where “&”-operator is defined and the corresponding subtraction is also optimized within the negation domain which instantly leads to the apposition of the label mark for each iteration – thus, the DFA can be also formed from NFA using this method without loss of generality like the upper bound of the automaton number of states within the effect, known as state explosion which was also well studied before [5].

From the above it follows that the state explosion can be avoided if we imply the complement operator and rewriting rule for subtraction “– “-operator while holding the positive output to be equal to the constant of one.

The ACO presented in is a modern and popular method for solving NP-complete problems [6, 7]. We will further give a universal approach for solving these problems using Dorigo’s et al. method for broad NP-complete problems like, for instance, vertex cover problem or VCP [8].

We will also give the notion to the Fisher’s experimentation with arbitrary number of factors – in this method the correlation between subset of factors plays the general role of distinguishing the positive or negative output in comparable frame of values which together form a powerset of size 2ⁿ [9].

Negation domains

These domains which were discussed before and, thus, represent the domain along the NFA which is then superseded by the DFA in subset construction – we hold this domain for generally the Kleene closure or star “*”- operator

It’s important to learn that Kleene closure leads to the source state in NFA to be traversed random number of runs and, thus, can be visited by the variable path while the general constraint isn’t satisfied like the difference between two languages in left and right edge leading to the source state in NFA.

These negation domains within the single output of the NFA using the method above leads to the proper construction of the output DFA for further storage and evaluation, while the star operator isn’t omitted and, thus, is presented anywhere without loss of generality and accepting language by the source regular expression, from which the NFA is constructed.

It’s enough to say that intersection and its NP-completeness was presented before and, thus, depends on the nature of the input regular expression – we advance this problem and get the stable and optimal results which are polynomial in nature and, thus, can be solved on any Turing tape automaton as well as verified in the same time [10].

The expression (1) was first implemented in Brics automaton Java-software package by Anders Moeller for general computations while the negation operator is implemented as a bi-simulated type of automata which were well studied in the past works – for now this is a dual question of using the negation domains or DFA implication within the Cartesian product of the automata from left and right subexpression of the complement or subtraction operator – this is both winning strategies which lead to a very quick and positive outcome.

Unified aco

The unified ACO can be represented by the following starting operation for two matrices:

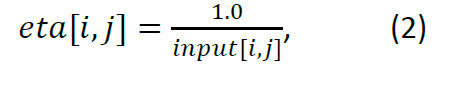
Where “eta” is a pheromone matrix and “input” is a matrix of the input data which are to be defined before the modeling ACO for optimization problem solution.

Another matrix which is to be defined as is:

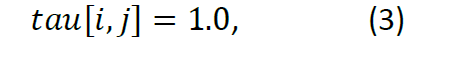
This is a compound matrix which defines the operation of each of the simulated agent like artificial ants. During each iteration we define the next candidate to be chosen according to the following optimization function:

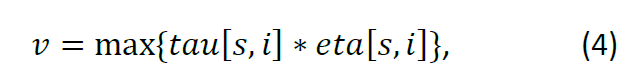
When the candidate v is chosen the matrix is updated according to the following rule:

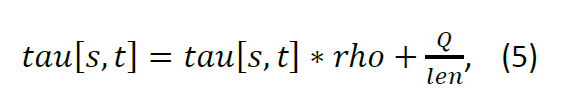
Where “rho” (between 0 and 1) and “Q” (between 0 and 100) are arbitrary parameters and “len” is the optimization function along the computed path of the selected candidates.

Universal approach of solving hard-problems without quantum computing or other means is the general acceptance of the artificial intelligence and solution of the so-called NP-hard or NP-complete problems which are also closed under EXPSPACE and EXPTIME.

The equations (2-5) are important to learn as they represent the inner output of the ACO algorithm in the main iteration which can be fixed or infinite and usually converges after pre-defined number of steps which is equal to the number of the size of the output.

To be clear we know that swarm optimization is a common term for ACO which is more simple to implement and our key result is to represent the unified form of this algorithm for further framework-like implementation which is already done in “AntTSP”-software package.

Discrete fractal numbers

The discrete fractals are defined as the recursive combined structures which can be used in image compression and other applications like the representation of the artificial objects on isometric plane. We define the discrete fractal as the relation to number “Pi”, when the number of output edges along the diametral distance is computed using module operator [11, 12].

This number can be used in the definition of the mathematical constant “Pi” divided by the diameter of the fractal tree.

Thus, recursive fractal is composed from the leaf-nodes and, thus, is propagated further using its structure as a graph.

We denote “Pi”-constant here as the lying border between its real and discrete value for fractal numbers on the recursive fractal tree which is infinite in states and has the property of the convex polygon on the discrete metrics as well as other types of data structures like trees and graphs.

Fisher’s experimentation

For the Fisher’s theory we define the superset which is defined as each subset of the factor set, thus giving the possibility of discrete optimization along each iteration of the algorithm on the pre-defined scale of the power set of these factors.

From the above it follows that the exponential complexity of the correlation computing between input factors cannot be avoided and we have probably to pertain to fuzzy solution or the solution implying the quantum computing which is well studied for now and has a wide application in the problems within exponential blow up complexity. Thus, the experimentation isn’t that easy, however, the control process can be tuned and other complexity can be devised from the correlated factors – the fact of correlation is to be devised as well as the factor tuning along the scale order which is defined in Fisher’s theory of planning the experiment.

Conclusion

Thus, we have defined the notion of subtraction or complement domains along the extended regular expressions which are implemented in “Regex+” software package – this gives a broad perspective of efficiently compute the DFA from Extended NFA for these operators and behave in the model of single output or full implication of the corresponding DFA into the NFA without loss of generality like acceptance of the regular language and its precise modelling on the DFA during linear search for the best performance in the matching input string.

We have also given the first ever known unified algorithm for Marco Dorigo’s ACO algorithm in order to solve the NP-complete problems within the fuzzy frame and less amount of time which is corrected by the number of iterations in the general phase.

The Fisher’s experimentation for each factor leads to exponential growth of the correlating elements and thus is to be computed using general approach like powerset encoding using bitmasks or bit-sets in modern programming languages like C++.

Fractals can be composed to the discrete “Pi”-constant, which is also shown in this article. Thus, the main ideas described in this work are to be evaluated from the modern point of view where the problems are to be solved using universal framework and the underlying problems are to be classified using the previous works on the automata or other data structures.

Acknowledgements

The author expresses gratitude to the staff of Satbayev University for giving all the necessary knowledge in order to open new perspectives and horizons of the bi-simulated and adaptive learning like ACO or Fisher’s experimentation methodology

We also express gratitude to the member of IntechOpen, Ivana Barac, for her interest in polynomials and other fields of Computer Science.

We are also very grateful to the ResearchGate™ community for vital comments

Funding

This work was fully supported by an educational grant of the Ministry of Education of Republic of Kazakhstan during author’s study from 2001 to 2006 at Satbayev University and from 2006 to 2009 at the Institute of Problems in Informatics and Control, al-Farabi Kazakh National University

References

1. Syzdykov, M. “Deterministic automata for extended regular expressions.” Open Comput Sci. 7.1 (2017): 24-28.

   [Google Scholar] [CrossRef]

2. Syzdykov, M. “Extended Regular Expressions in Finite Automata Revisited.” Adv. Technol. And Comput. Sci. 1. (2022): 4-7.

   [Google Scholar]

3. Pin, Jean-Éric. "An explicit formula for the intersection of two polynomials of regular languages." DLT (2013): 31-45.

   [Google Scholar] [CrossRef]

4. Rabin, Michael O., and Dana Scott. "Finite automata and their decision problems." IBM J Res Dev. 3.2 (1959): 114-125.

   [Google Scholar] [CrossRef]

5. Syzdykov, Mirzakhmet. "Equivalence of Complexity Classes via Finite Automata Derivatives." Adv Technol and Comput. Sci. 1.4 (2022): 9-14.

   [Google Scholar]

6. Dorigo, Marco, et al. "Ant colony optimization." IEEE 1.4 (2006): 28-39.

   [Google Scholar] [CrossRef]

7. Asif, M, & Rauf B. "Solving NP-complete problem using ACO algorithm." IEEE. (2009) 13-16.

   [Google Scholar] [CrossRef]

8. Shyu, Shyong Jian, et al. "An ant colony optimization algorithm for the minimum weight vertex cover problem." Ann Oper Res. 131 (2004): 283-304.

   [Google Scholar] [CrossRef]

9. Xygkis, Themistoklis C., et al. "Fisher information-based meter placement in distribution grids via the D-optimal experimental design." IEEE. 9.2 (2016): 1452-1461.

   [Google Scholar] [CrossRef]

10. Fürer, Martin. "The complexity of the inequivalence problem for regular expressions with intersection." In Automata, Languages and Programming. (1980). 234-245.

    [Google Scholar] [CrossRef]

11. Tong, Chong-Sze, & Minghong Pi. "Fast fractal image encoding based on adaptive search." IEEE 10.9 (2001): 1269-1277.

    [Google Scholar] [CrossRef]

12. Syzdykov, Mirzakhmet. “Theory of Noise with Applications: A Practical and Theoretical Guide.” LAP LAMBERT Acad. Publ. 2016.

    [Google Scholar] [CrossRef]