International Journal of Computer Science and Mobile Applications

Design and Analysis of a Plasmonic Refractive Index Sensor with Symmetrical Cavities and Rings

Hamid Abbasi^* University of Mazandaran, Iran
^*Correspondence: Hamid Abbasi, University of Mazandaran, Iran, Email:

Received: Mar 31, 2023, Manuscript No. ijcsma-23-93693; Editor assigned: Apr 01, 2023, Pre QC No. ijcsma-23-93693 (PQ); Reviewed: Apr 08, 2023, QC No. ijcsma-23-93693 (Q); Revised: Apr 14, 2023, Manuscript No. ijcsma-23-93693 (R); Published: Apr 20, 2023, DOI: 10.5281/zenodo.8058379

Introduction

Plasmonics is an emerging, interdisciplinary discipline that combines materials science, physics, Nano photonics, and computational simulation to detect many phenomena. Our aim in this paper is to investigate and improve the properties of a plasmonic refractive index Nano sensor based on surface plasmon resonance technology by finite difference time domain method and then measure its performance using refractive index change. For this reason, proper sensor configuration, determination of data, dimensions and coordinates of amplifiers and accurate calculation of sensitivity, Figure of Merit (FOM) and Q quality factor are of particular importance. Plasmon Surface Polaritons (SPPs) are also electromagnetic fields that propagate along the metal insulation interface and have been noted for their ability to modulate light at the nanoscale and break the diffraction limit. Therefore, plasmon surface can be increased in many fields such as increase in adsorption [1,2], photocatalysis [3-8], increase of magnetic field [9,10], THz oscillation [11-13], fano resonance [14-17], surface Raman scattering SERS [18-21], below-wavelength lithography [22,23] and refractive index sensors [24-29]. Plasmonic coefficient sensors, meanwhile, have attracted more attention because they are much smaller in size comparable to sensor performance, meaning they are more suitable for integration. By changing the dimensions and coordinates of the resonators, we come to the conclusion that the closer the distance between them to the waveguides and to the intermediate amplifier, the greater the sensitivity coefficient and will have a greater impact on improving sensor quality. Also, in all simulations, we only change the refractive index of the intermediate resonator located between the two waveguides, and the refractive index of the other resonators remains constant, as this improves the quality of the sensor and more accurate evaluation. Its performance will be [30]. According to calculations, the highest sensitivity is 6160 nm / RIU, which is higher than similar sensors.

Literature Review

Structural Model and Theory Analysis

Figure 1 shows a two-dimensional image of the proposed refractive index sensor. This sensor consists of two waveguides, nine rings and eighteen cavities. The height of two plasmonic waveguides is equal to w=50 nm. The middle ring has an inner radius of r1=81 nm and an outer radius of R1=140 nm and its distance with two waveguides is 10 nm. The other eight rings are located above and below the waveguides and has internal radius r2 = r3 = r4 = r5 = r6 = r7 =r8 = r9 = 91 nm and the external radius R2 = R3 = R4 = R5 = R6 = R7 = R8 = R9= 126 nm and each of these rings is connected to one of the cavities. The cavities w1, w2, w3, w4, w6, w7, w8, w11, w12, w13, w14, w15 and w16 have a height of 150 nm and a length of 30 nm. The w9 and w10 cavities are 417 nm high and 30 nm long. The cavity w5 has a height of 630 nm and a length of 30 nm. The cavity w18 has a height of 1670 nm and a length of 30 nm.

Figure 1: Proposed Structure for Refractive Index Sensor

Also, two monitors, Pin and Pout, will be used to measure the input and output waves. The wave transmission rate will be calculated by the following equation:

To study the wave transmission in the designed sensor, we use a metal-based structure built on the surface Plasmon polariton and apply Maxwell equations at the interface between a metal and a dielectric. Therefore, we conclude that only TM transverse magnetic polarization participates in wave transmission. This conclusion is obtained by examining the relationship between the scattering of incoming light and considering that the height of the waveguide is smaller than the wavelength of the incoming light. The scattering relationship of this condition is expressed as follows [31]:

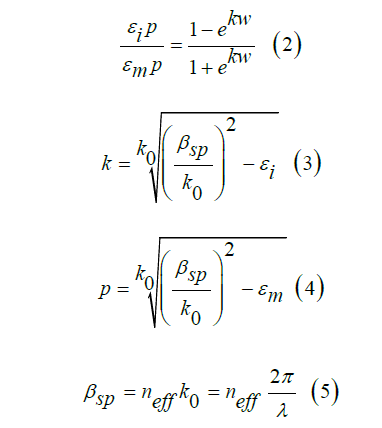
Here, ω width causes λ wavelength of light in a vacuum. β_sp and n_eff are effective constants and refractive index of SPPs. ε_i and ε_m give the relative dielectric permittivity of metal and k₀ =2π/λ means the number of waves.

Sensor Simulation and Design Methods Using Refractive Index Measurement

The resonant behavior of the proposed sensor structure is investigated by both numerical and theoretical methods. In the numerical method, we will use the time domain finite difference simulation method with perfectly matched layer boundary conditions PML. Because this method will effectively reduce the numerical reflection. In the mesh of this simulation, x and y are equal to 8 nm. Also, the transmission line model is used to analyze the theory of structure [32,33]. To achieve a better result and reduce the sensor simulation time, we need to do the simulation in two dimensions. This simulation will be calculated in the wavelength range of 500 nm to 1500 nm. We use the drude model to show the optical properties of metals in simulation. Because the drude model can be easily integrated into time-difference finite difference simulations:

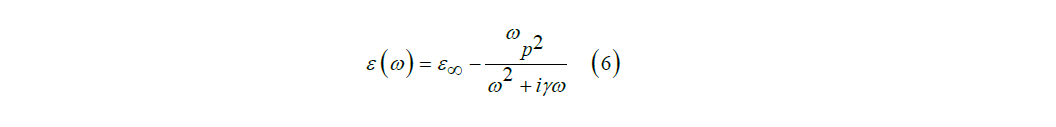
Here, ω shows incident light angular frequency, ε_∞ =1 gives the medium constant for the infinite frequency, ω_p = 1.37 × 1016 refers to bulk frequency for plasma and γ = 3.21 × 1013 means damping frequency for electron oscillation. The TM input wave starts moving from the left and will propagate in the waveguide. The closer this wave is to the output, the lower its intensity. If the input wave momentum matches the surface plasmon momentum, the input wave can stimulate the surface plasmon. As a result, a diffusion and longitudinal polarization are obtained. To start the simulation; we first do the work with a ring and several cavities. In the second step, we remove all the cavities from the structure and do the simulation only with the rings. Finally, we put all the resonators (cavities and rings) together in the simulation to fully examine the proposed sensor structure. That is, the type and number of resonators and their dimensions and coordinates help us to design a functional sensor and to examine the performance of this sensor in detail.

Simulation and Design of a Sensor Using Two Waveguides, Sixteen Cavities and A Ring

The proposed sensor is designed with two waveguides, sixteen cavities and a ring (Figure 2).

Figure 2: Proposed Structure for the Designed Refractive Index Sensor, Consisting of Two Waveguides, Sixteen Cavities and a Ring.

The refractive index of waveguides and cavities remains constant and we change the refractive index of the middle ring. We change the refractive index of the middle ring with steps of 0.01 nm from n=1.08 to n=1.13. The transmission spectrum of the sensor structure has two peaks. The left peak has a higher height and a narrower FWHM. At the right peak, the rate of wavelength change is greater, so the right peak is more sensitive (Figure 3).

Figure 3: Transmission Spectrum of the Plasmonic Structure with Sixteen Cavities and a Ring

We can use three criteria to evaluate the performance of the designed sensor. The first criterion is the sensitivity S, which is described as the change in resonance wavelength when the refractive index changes:

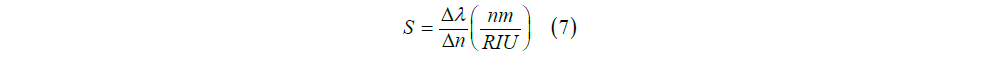
In this equation, â??λ is the resonance wavelength change, â??n is the refractive index change. We see the sensitivity coefficient diagram of the designed sensor in Figure 4. According to the figure, the maximum sensitivity for the refractive index is n=1.11 (in mode 2), which is equal to 1438 nm / RIU. According to this diagram, the peak on the right has a balanced increase in wavelength and sensitivity. Thus there is a linear relationship between the two resonant wavelength parameters and the refractive index.

Figure 4: Sensitivity Diagram of a Designed Sensor with Sixteen Cavities and a Ring

We draw the field distribution for the wavelength that is most sensitive. According to Figure 5, the maximum radiation is in the middle ring. The interesting thing is that the cavities on the left absorb more energy than the cavities on the right and have more exchange with the input wave. Of course, all the cavities in the sensor structure absorb part of the input wave, which proves that the designed sensor has an optimal structure.

Figure 5: Display of Field Distribution |Hz| in Structure at the Resonance Wavelength

The second criterion is the Figure of Merit(FOM) and its equation is as follows:

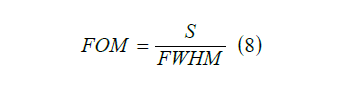
The Figure of Merit (FOM) diagram for the plasmonic sensor, it is drawn in Figure 6. According to the figure, the maximum Figure of Merit (FOM) for the refractive index is n=1.11 (in mode2), which is equal to 10.27 nm / RIU.

Figure 6: Figure of Merit(FOM) for the Proposed Sensor

The third criterion is the quality factor Q, which is obtained according to Equation 9 comes:

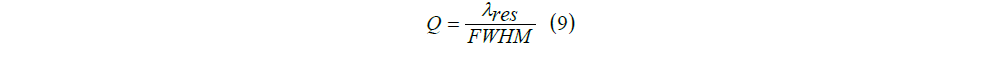
The diagram of the plasmonic sensor quality factor is shown in Figure 7. According to the figure, the highest quality factor Q is for the refractive index n=1.3 (in mode1), which is equal to 16. 05.

Figure 7: Designed Sensor Quality Factor Diagram

Simulation and Design of a Sensor Using Two Waveguides, Nine Rings

The proposed sensor is designed with two waveguides and nine rings (Figure 8).

Figure 8: Two-Dimensional Image of the Designed Refractive Index Sensor, Consisting of Two Waveguides and Nine Rings.

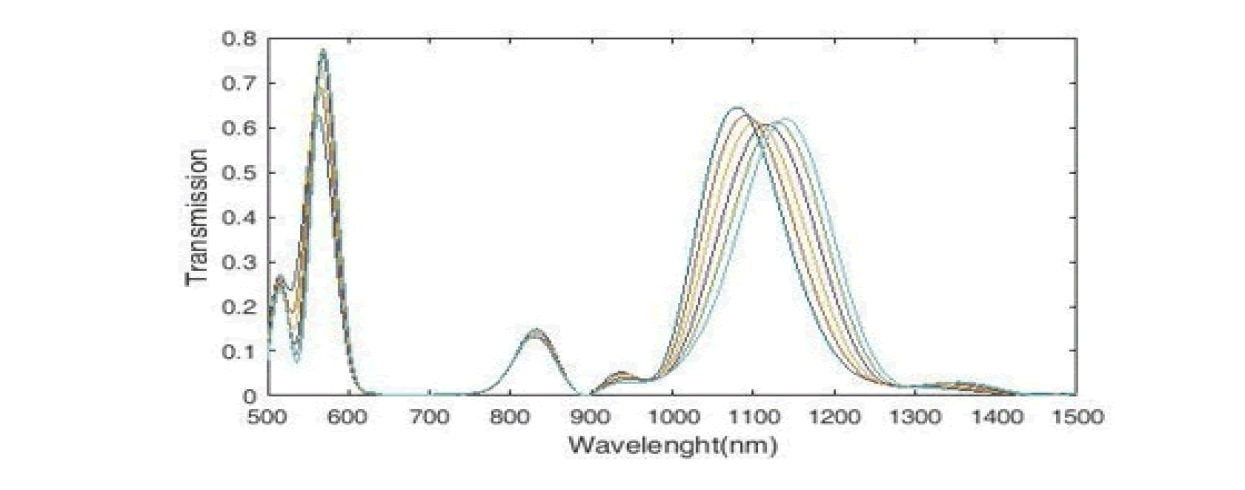
The refractive index of the waveguides and the eight upper and lower rings remain constant and we change the refractive index of the middle ring. We change the refractive index of the middle ring with steps of 0.01 nm from n =1. 08 to n=1.13. The transmission spectrum of the sensor structure has two peaks. The left peak has a higher height and a narrower FWHM. At the peak on the right, FWHM is wider and the change in wavelength is greater, so the peak on the right is more sensitive and shows better performance (Figure 9).

Figure 9: Transmission Spectrum of the Plasmonic Structure with Nine Rings.

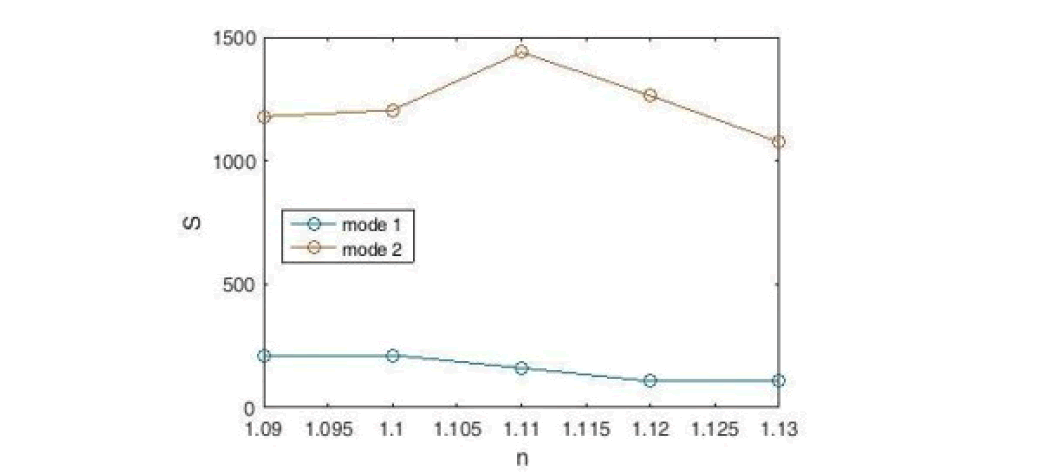
We see the sensitivity diagram of the desired sensor in Figure 10. According to the figure, the maximum sensitivity for the refractive index is n=1.09 (in mode2), which is equal to 1183 nm/ RIU.

Figure 10: Sensitivity Diagram of a Designed Sensor with Nine Rings

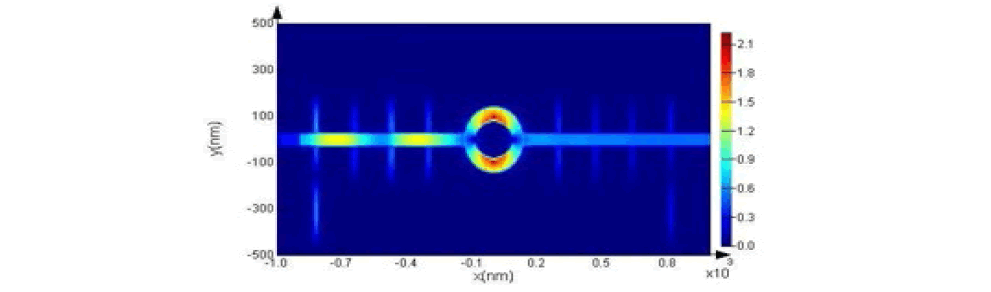
We draw the field distribution for the wavelength that is most sensitive. According to Figure 11, the maximum radiation is in the middle ring.

Figure 11: Display of Field Distribution |Hz| in Structure at the Resonance Wavelength.

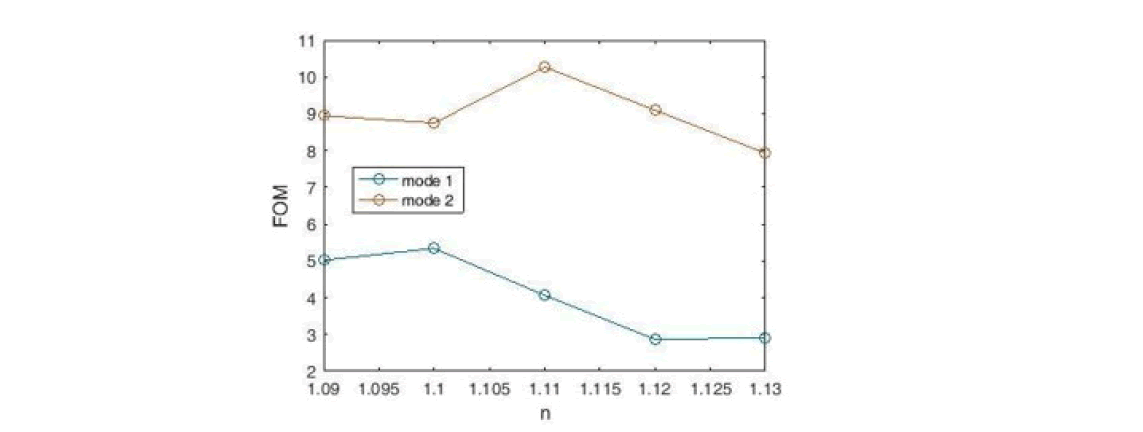
Using Equation 8, we plot the Figure of Merit (FOM) of the desired sensor (Figure 12). According to the figure, the maximum Figure of Merit (FOM) for the refractive index is n=1.1 (in mode2), which is equal to 43.73 nm / RIU. This amount of FOM is a significant increase over the previous sensor.

Figure 12: Figure of Merit(FOM) for the Proposed Sensor.

Using Equation 9, we plot the quality coefficient of the desired sensor (Figure 13). According to the figure, the highest quality factor Q for the refractive index is n=1.1 (in mode 2), which is equal to 60.01, which is a significant increase over the previous sensor.

Figure 13: Designed Sensor Quality Factor Diagram.

Simulation and Design of the Sensor Using Two Waveguides, Eighteen Cavities and Nine Rings

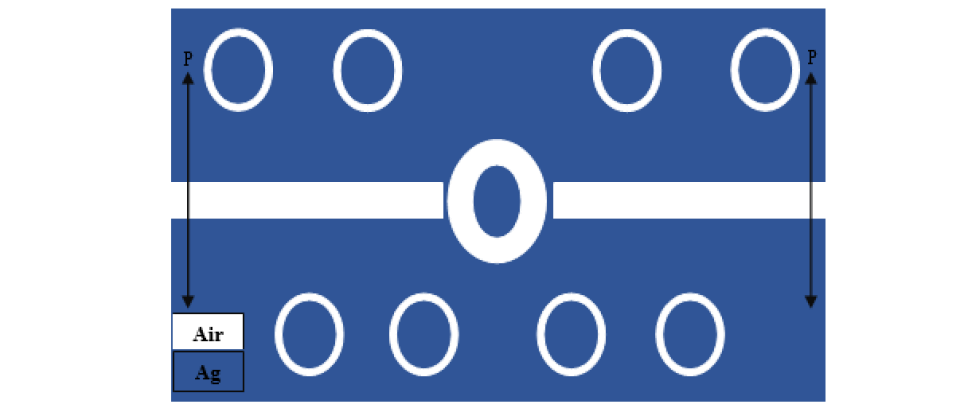
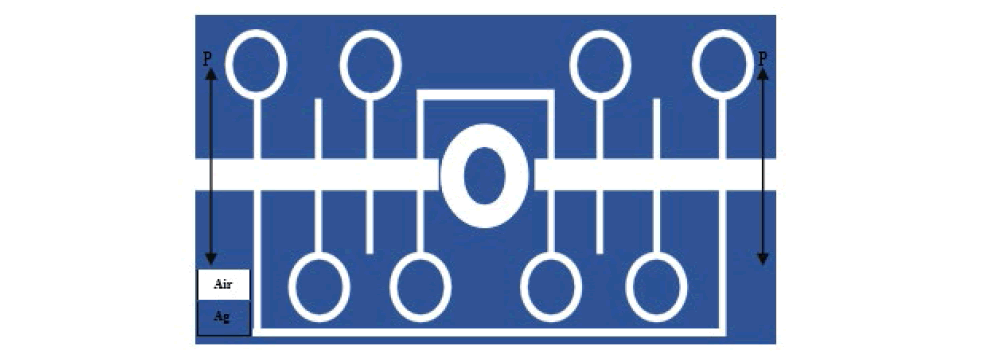
The proposed sensor is designed with two waveguides, eighteen cavities and nine rings (Figure 14). Here, we combine the structure of the previous two sensors to achieve better results. The refractive index of waveguides and cavities remains constant and we change the refractive index of the middle ring. We change the refractive index of the middle ring with steps of 0.01 nm from n =1. 08 to n = 1.13.

Figure 14: Two-Dimensional Image of a Designed Refractive Index Sensor, Consisting of Two Waveguides, Eighteen Cavities and No Rings

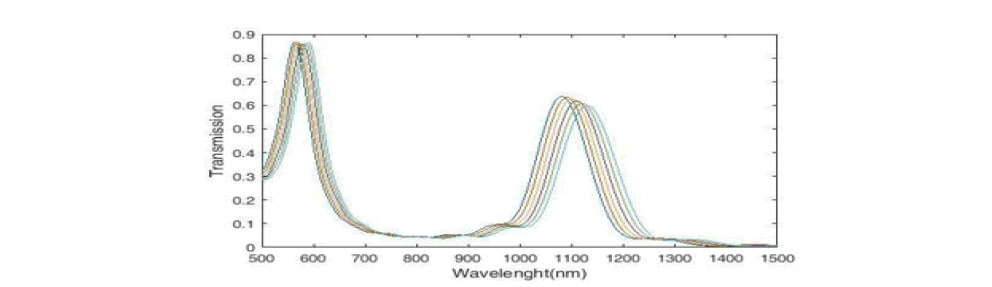
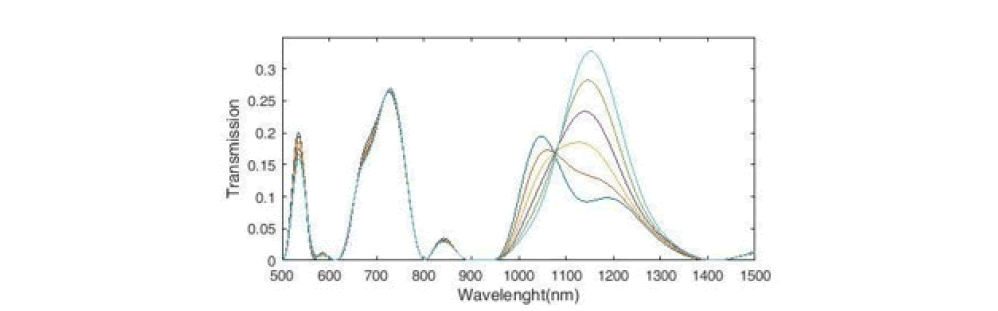
The transmission spectrum of the sensor structure has three peaks. The courier on the left has the narrowest FWHM. The middle peak has the highest height. The peak on the right has a wider FWHM and has a much larger wavelength change. The type of sensor structure and the extremely high rate of wavelength change indicate that this sensor has a very good performance and quality compared to similar sensors and will be very useful in the manufacture of military equipment and technological advances (Figure 15).

Figure 15: Transmission Spectrum of the Plasmonic Structure with Eighteen Cavities, Nine Ring.

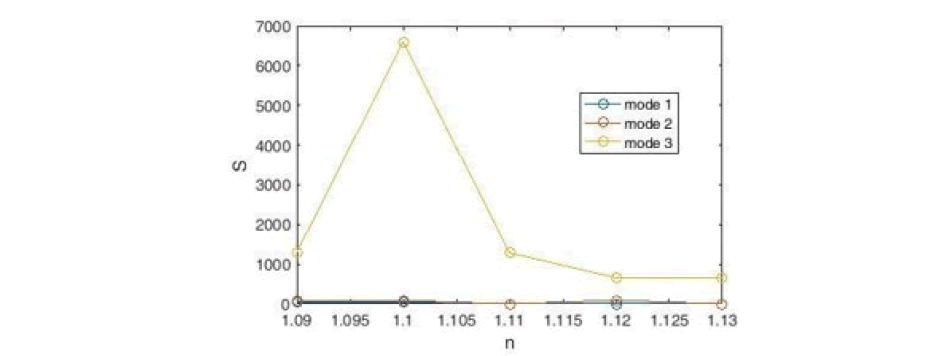
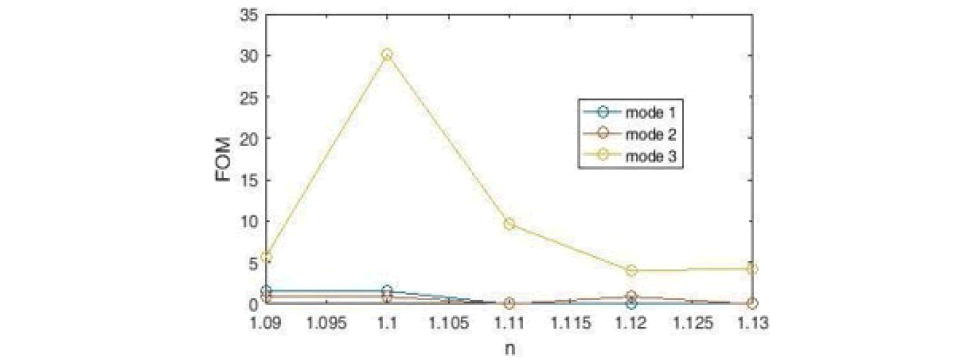
Using Equation 7, we plot the sensitivity coefficient of the designed sensor (Figure 16).

Figure 16: Sensitivity Diagram of a Designed Sensor with Eighteen Cavities, Nine Rings

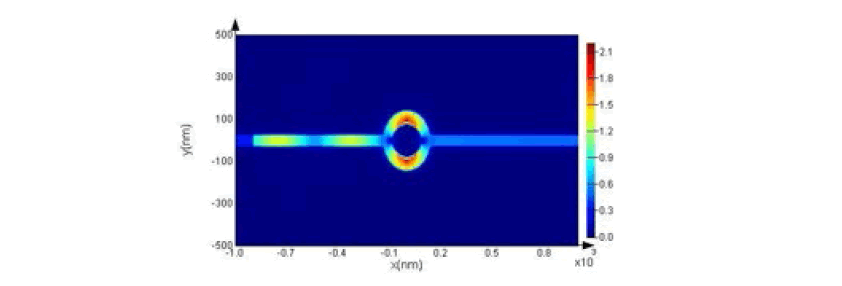
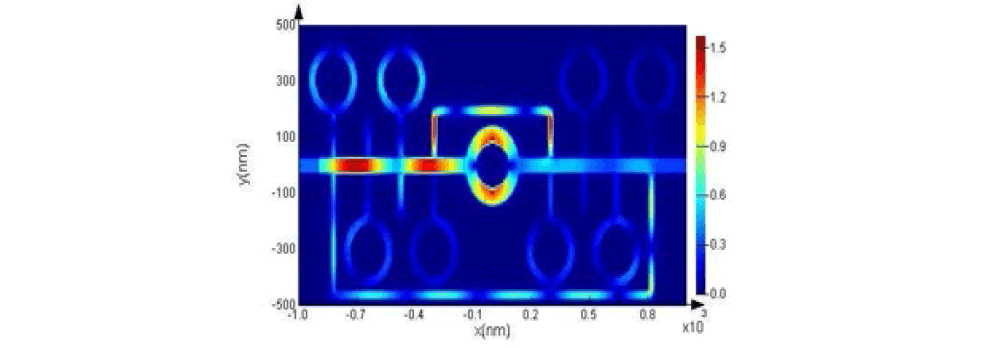
According to the Figure, the maximum sensitivity for the refractive index is n = 1.1 (in 3 modes), which is equal to 6591 nm / RIU. According to this diagram, the peak on the right has a very high and extraordinary increase in wavelength and sensitivity. We draw the field distribution for the wavelength that is most sensitive. According to Figure 17, the maximum radiation is in the middle ring and the middle cavity. Also, the distribution of the field with two rims on the left and three cavities at the bottom was appropriate and these resonators have also been successful in absorbing input energy. Of course, all the cavities in the sensor structure include part of the input wave, which proves that the designed sensor has an optimal structure.

Figure 17: Display of Field Distribution |Hz| in Structure at the Resonance Wavelength.

Using Equation 8, we plot the Figure of Merit (FOM) of the desired sensor (Figure 18). According to the figure, the maximum Figure of Merit (FOM) for the refractive index is n=1.1 (in mode3), which is equal to 30.12 nm / RIU. This amount of FOM is a significant increase over the previous sensor.

Figure 18: Figure of Merit(FOM) For the Proposed Sensor.

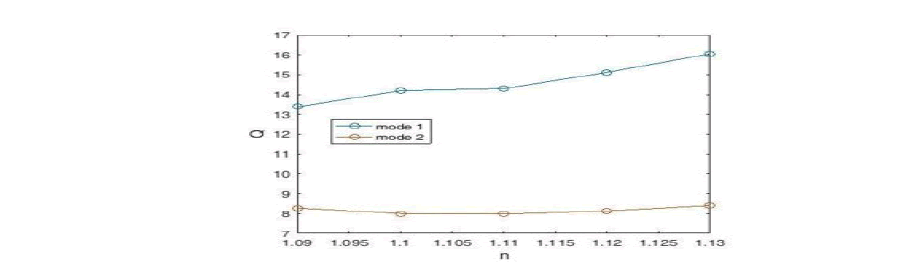
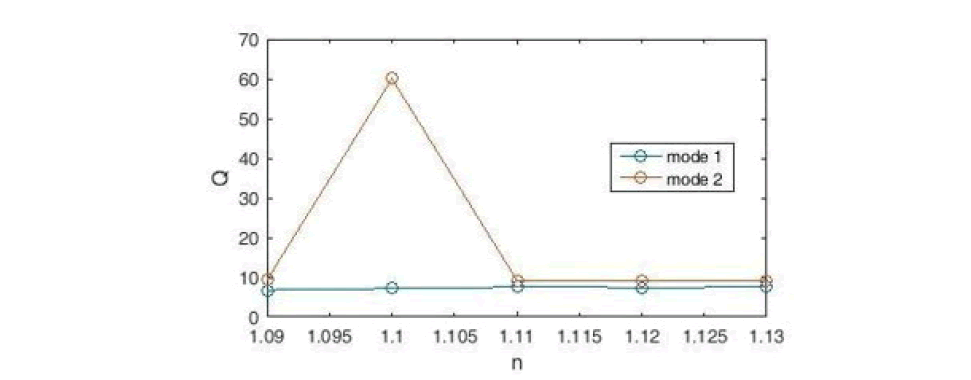
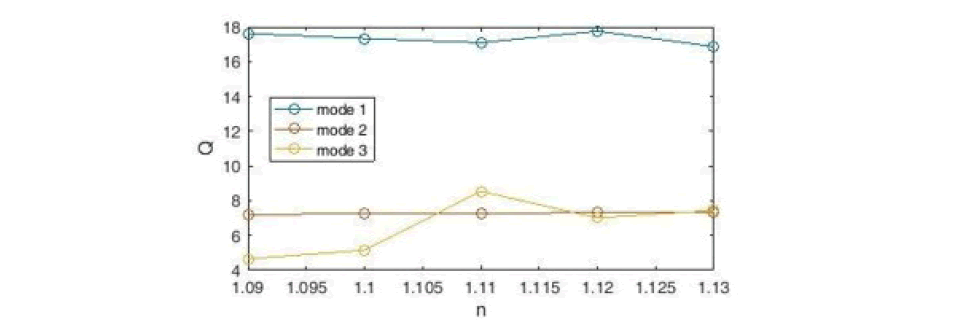
Using Equation 9, we plot the quality coefficient of the desired sensor (Figure 19). According to the figure, the highest quality factor Q is for the refractive index n = 1.12 (in mode 1), which is equal to 17.76.

Figure 19: Designed Sensor Quality Factor Diagram.

Conclusion

In this paper, a refractive index sensor based on plasmonic waveguide resonance is investigated. A resonator system connected to a plasmonic waveguide, consisting of two waveguides, nine cavities and eighteen rings, has been designed and investigated. The results show that the resonance wavelength will change dramatically with increasing and changing refractive index, which suggests that this method can be used to evaluate the performance of the proposed sensor. In the following, the sensitivity coefficient and the Figure of Merit (FOM) and the Q quality coefficient are examined, in which the highest sensitivity of the sensor is 6591 nm / RI. Also, the maximum Figure of Merit (FOM) is 43.73 nm / RIU and the highest quality factor Q is equal to 60.01. The calculations performed and the results obtained prove that this sensor has an excellent performance and it is more efficient than similar sensors.

Data Availability

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

Code Availability

Numerical analysis of this paper is based on FDTD method.

Compliance with Ethical Standards

Competing Interests The authors declare that they have no competing interests.

Funding Information

This study hasn’t any financial support.

Authors’ Contributions

All authors have same contribution in the analytical and numerical calculations and read and approved the final manuscript.

References

1. Cen, C., et al. "Tunable absorption enhancement in periodic elliptical hollow graphene arrays." Opt Mater Express 9.2 (2019): 706-716.

   [Google Scholar]

2. Lin, H., et al. "Plasmonic absorption enhancement in graphene circular and elliptical disk arrays." Mater Res Express 6.4 (2019): 045807.

   [Google Scholar]

3. Zhao, X., et al. "Synthesis and theoretical study of large-sized Bi4Ti3O12 square nanosheets with high photocatalytic activity." Mater Res Bull 107 (2018): 180-188.

   [Google Scholar] [CrossRef]

4. Di, L., et al. "Construction of Z-scheme g-C3N4/CNT/Bi2Fe4O9 composites with improved simulated-sunlight photocatalytic activity for the dye degradation." Micromachines 9.12 (2018): 613.

   [Google Scholar] [CrossRef]

5. Yan, Y., et al. "Enhanced photocatalytic activity of surface disorder-engineered CaTiO3." Mater Res Bull. 105 (2018): 286-290.

   [Google Scholar] [CrossRef]

6. Zheng, C., et al. "A novel Bi 4 Ti 3 O 12/Ag 3 PO 4 heterojunction photocatalyst with enhanced photocatalytic performance." Nanoscale Res Lett. 12 (2017): 1-12.

   [Google Scholar] [CrossRef]

7. Zhang, S., et al. "Enhanced photocatalytic activity of a visible-light-driven ternary WO3/Ag/Ag3PO4 heterojunction: a discussion on electron transfer mechanisms." RSC adv. 10.29 (2020): 16892-16903.

   [Google Scholar] [CrossRef]

8. Hou, W., and Stephen B. C. "A review of surface plasmon resonance-enhanced photocatalysis." Adv Funct Mater. 23.13 (2013): 1612-1619.

   [Google Scholar] [CrossRef]

9. Chen, Jing, et al. "Optical magnetic field enhancement via coupling magnetic plasmons to optical cavity modes." IEEE Photonics Technol Lett. 28.14 (2016): 1529-1532.

   [Google Scholar] [CrossRef]

10. Chen, J., et al. Surface-plasmonpolaritons- assisted enhanced magnetic response at optical frequencies in metamaterials. IEEE Photonics J. 2016, 8, 4800107.
11. Safari, S., and B. Jazi. "The role of terahertz surface plasmons in the scattering pattern of electromagnetic waves in an unstable elliptical plasma antenna." Phys Plasmas 24.7 (2017): 072112.

    [Google Scholar]

12. Hongmei, D. U., et al. "THz plasma wave instability in field effect transistor with electron diffusion current density." Plasma Science and Technology 20.11 (2018): 115001.

    [Google Scholar] [CrossRef]

13. Dongao, L. I., et al. "The instability of terahertz plasma waves in cylindrical FET." Plasma Sci Technol 21.4 (2019): 045002.

    [Google Scholar] [CrossRef]

14. Wang, J., et al. "Tunable Fano resonance based on grating-coupled and graphene-based Otto configuration." Optics Express 25.20 (2017): 23880-23892.

    [Google Scholar]

15. Zhang, X., et al. "Refractive index sensor based on fano resonances in plasmonic waveguide with dual side-coupled ring resonators." Photonic Sens 8 (2018): 367-374.

    [Google Scholar] [CrossRef]

16. Piao, X., et al. "Fano-type spectral asymmetry and its control for plasmonic metal-insulator-metal stub structures." Optics express 19.11 (2011): 10907-10912.

    [Google Scholar] [CrossRef]

17. Piao, X., et al. "Control of Fano asymmetry in plasmon induced transparency and its application to plasmonic waveguide modulator." Optics express 20.17 (2012): 18994-18999.

    [Google Scholar] [CrossRef]

18. Liu, G. Q., et al. "One-process fabrication of metal hierarchical nanostructures with rich nanogaps for highly-sensitive surface-enhanced Raman scattering." Nanotechnology 26.18 (2015): 185702.

    [Google Scholar] [CrossRef]

19. Xiang X. W., et al. "Surface-enhanced Raman scattering effect of composite structure with gold nano-cubes and gold film separated by polymethylmethacrylate film." (2019).

    [Google Scholar] [CrossRef]

20. Yu, M., et al. "Annealed gold nanoshells with highly-dense hotspots for large-area efficient Raman scattering substrates." Sens Actuators B: Chem 262 (2018): 845-851.

    [Google Scholar] [CrossRef]

21. Wang, X., et al. "Investigation of surface plasmons in Kretschmann structure loaded with a silver nano-cube." Results Phys. 12 (2019): 1866-1870.

    [Google Scholar] [CrossRef]

22. Tong, H., et al. "Theoretical study for fabricating elliptical subwavelength nanohole arrays by higher-order waveguide-mode interference." Results Phys. 14 (2019): 102460.

    [Google Scholar] [CrossRef]

23. Wang, X., et al. "Theoretical investigation of a highly sensitive refractive-index sensor based on TM0 waveguide mode resonance excited in an asymmetric metal-cladding dielectric waveguide structure." Sensors 19.5 (2019): 1187.

    [Google Scholar] [CrossRef]

24. Liang, C., et al. "Tunable triple-band graphene refractive index sensor with good angle-polarization tolerance." Opt Commun. 436 (2019): 57-62.

    [Google Scholar] [CrossRef]

25. Liu, C., et al. "Symmetrical dual D-shape photonic crystal fibers for surface plasmon resonance sensing." Optics express 26.7 (2018): 9039-9049.

    [Google Scholar] [CrossRef]

26. Liu, Z., et al. "Enhancing refractive index sensing capability with hybrid plasmonic–photonic absorbers." J Mater Chem. C 3.17 (2015): 4222-4226.

    [Google Scholar]

27. Yun P. Q., et al. "Refractive index sensor and filter of metal-insulator-metal waveguide based on ring resonator embedded by cross structure." (2018).

    [Google Scholar] [CrossRef]

28. Cen, C., et al. "A tunable plasmonic refractive index sensor with nanoring-strip graphene arrays." Sensors 18.12 (2018): 4489.

    [Google Scholar] [CrossRef]

29. Liu, C., et al. "Mid-infrared surface plasmon resonance sensor based on photonic crystal fibers." Optics express 25.13 (2017): 14227-14237. [Google Scholar]

    [CrossRef]

30. Wang, X., et al. "Theoretical investigation of a highly sensitive refractive-index sensor based on TM0 waveguide mode resonance excited in an asymmetric metal-cladding dielectric waveguide structure." Sensors 19.5 (2019): 1187.

    [Google Scholar] [CrossRef]

31. Maier, S. A. Plasmonics: fundamentals and applications. N Y: springer, 2007.

    [Google Scholar]

32. Gierak, J., et al. "Sub-5 nm FIB direct patterning of nanodevices." Microelectron eng. 84.5-8 (2007): 779-783.

    [Google Scholar] [CrossRef]

33. Wu, W., et al. "Ultra-high resolution filter and optical field modulator based on a surface plasmon polariton." Opt Lett. 41.10 (2016): 2310-2313.

    [Google Scholar] [CrossRef]